半環でグラフとサンバを

ちょっと前に半環とグラフに関する面白い話題を得たので、忘れないうちに書いておこうと思います。
猛暑がつづく悲しき亜熱帯に捧げる、トロピカルな記事です。

概要

一般に無閉路有向グラフ (DAG) は隣接行列の形で表すことができますが、隣接行列の累乗の和を計算すると、すべての二頂点間の経路重みの総和を計算することができます。実はこの計算過程をちょっと変えて、半環の一種であるトロピカル半環を用いると、すべての頂点間の最短経路が求められるというお話です。

隣接行列の積で経路重みの総和を計算

与えられた無閉路有向グラフ (以下、単にグラフ) のすべての二頂点間の経路重みの総和を計算しようと思ったとき、そのグラフの隣接行列の累乗の和を計算するという方法が使えます。ここで経路重みの総和とは、ある始点からある終点までの各経路について、同じ経路上の辺の重みを乗算し、それらの結果をすべて足し合わせたものとします。

例えば以下のような重み付きDAGを考えます。

f:id:hark00:20140801142038p:plain:w180

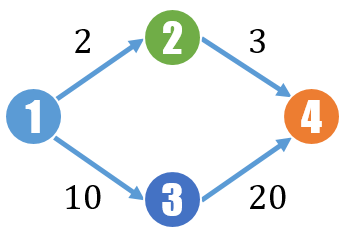
頂点 1 から頂点 4 までの経路は 2 本あります。それぞれの経路の重みは 2 × 3 = 6 と 10 × 20 = 200 で、これらを足した 206 が頂点 1 から頂点 4 までの経路の重みの総和です。

では、経路重みの総和をグラフの隣接行列の累乗の和から求めてみます。上図のグラフの隣接行列 M は以下のようになります。

$M = \begin{pmatrix} 0 & 2 & 10 & 0 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 20 \\ 0 & 0 & 0 & 0 \end{pmatrix}$

次に累乗の和を計算してみます。

$M^{*} = \sum_{n\in\mathbb{N}} M^{n}$

グラフの直径を r とすると、n > r の場合の M の n 乗は零行列になりますので、以下の計算では無視しています。上のグラフの直径は 2 なので、n = 2 まで計算すれば十分です。なお、閉路のあるグラフでは、n = k のとき長さ k 以下の経路の重みの総和が求められます。

f:id:hark00:20140804194304p:plain:w300

これですべての二頂点間の経路重みの総和が計算できました。図にある通り、頂点 1 から頂点 4 への経路重みの総和は、1 行目の 4 列目を見ればよいので、206 であることがわかります。

最短距離の計算

この節ではグラフの重みを距離と解釈します。前節での計算方法をちょっと変えると、ほぼ同じ手順で二頂点間の最短距離を求めることができます。変える部分は主に以下の3点です。

0 を $\infty$ で置換する
行列の任意の2要素 x, y の乗算 xy の代わりに加算 x + y を計算する
行列の任意の2要素 x, y の加算 x + y の代わりに min(x, y) を計算する

例で説明します。通常の行列の演算では、

$A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix},\ B=\begin{pmatrix} 10 & 20 \\ 30 & 40 \end{pmatrix}$

の加算と乗算は

$A+B=\begin{pmatrix} 1+10 & 2+20 \\ 3+30 & 4+40 \end{pmatrix}, \ A\times B=\begin{pmatrix} 1\cdot 10 + 2\cdot 30 & 1\cdot 20 + 2\cdot 40 \\ 3\cdot 10 + 4\cdot 30 & 3\cdot 20 + 4\cdot 40 \end{pmatrix}$

です。よって

$A+B=\begin{pmatrix} 11 & 22 \\ 33 & 44 \end{pmatrix},\ A\times B=\begin{pmatrix} 70 & 100 \\ 150 & 220 \end{pmatrix}$

となります。一方、上の変更を適用すると、行列間の加算は

$A+B=\begin{pmatrix} \min(1,10) & \min(2,20) \\ \min(3,30) & \min(4,40) \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$

となり、また乗算は

$A\times B=\begin{pmatrix} \min(1+10,2+30) & \min(1+20,2+40) \\ \min(3+10,4+30) & \min(3+20,4+40) \end{pmatrix} = \begin{pmatrix} 11 & 21 \\ 13 & 23 \end{pmatrix}$

となります。では、このようなルールで $M^*$ を計算してみましょう。

f:id:hark00:20140804195651p:plain:w300

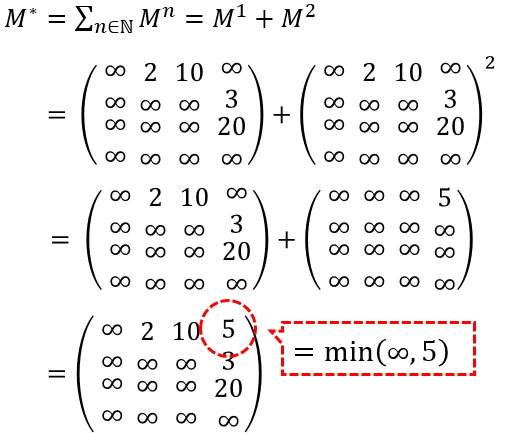
計算結果を見ると、行列の各要素が二頂点間の最短距離になっていることがわかります。1 行目の 4 列目は 5 ですが、これは頂点 1 から頂点 4 までの最短距離に対応しています。実際、上のグラフを見ると頂点 1 から頂点 4 までの最短距離は 2 + 3 = 5 となっています。

半環とトロピカル半環

経路重みの総和を求めた最初の例は、非負の実数上の4次正方行列半環を土台としており、最短経路を求めた例は、非負の実数上のトロピカル半環が土台です。

環はおおざっぱにいうと加法（加算）と乗法（乗算）の二種類の二項演算を持つ代数的構造です。また、加法的逆元を持たない環を半環と呼びます。
半環の中でも、加法として min を、乗法として $+$ を持つ半環をトロピカル半環と呼びます。

上記の2つの例は加法と乗法の定義が異なっていただけで、計算の手続きは一緒でした。
ということは、経路重みの総和を計算するコードを書いておけば、重みに対する演算子のふるまいを変えるだけで、同じコードから最短経路が求められるようになります。かっこいい。

以上の話を発展させると「最短経路問題のための汎用アルゴリズム」が得られ、よく知られているダイクストラ法やベルマン・フォード法はこの汎用アルゴリズムの特殊な場合となります。
詳細は以下の論文をご参照ください。

Mohri, M. (2002). Semiring frameworks and algorithms for shortest-distance problems. Journal of Automata, Languages and Combinatorics, 7(3), 321-350. [ pdf ]