2018年の思い出

2018年は、2014年から4年も放置したこのブログを再開した。といっても記事はほとんど書いていないが、個人的には大きな一歩である。

仕事では非常に大規模かつミッションクリティカルなシステムの開発プロジェクトに関わった。主にC++とPythonを書いていた。優秀な方々と働くことができたので、楽しかった。

また、いくつかのCourseraのコースを受講して修了した。どれも教材の質が高く、苦にならなかった。

面白かった本

各本のリンクは出版社のWebページへのリンク。

エレンディラ（G．ガルシア＝マルケス）

「大人のための残酷物語として書かれた」って説明だけでときめく。短編集なので、日常的な超常というか、上質なマジックリアリズムを手軽に摂取できる本。

すばらしい新世界（オルダス・ハクスリー）

ディストピアものとして有名な作。光文社古典新訳文庫版の翻訳がとても良い。同じディストピアものの『1984』と比べると、生前に各個人の能力が階級別に分けられる点で、こちらの方が怖いと思う。この本の設定をもっと現実的にすると映画『ガタカ』になる感じ。

本のエンドロール（安藤祐介）

「紙の本ができるまで」に関わる人々に焦点をあてた小説。紙の本の市場が縮小傾向で苦労する印刷所の営業マンが主人公。「出版」に関して知りたかったことが書かれていてとてもよかった。とあるビブリオバトルでは、この本を泣きながら紹介する業界関係者の方がいたとか。現実の、この本ができるまでの過程が動画で公開されており、本文で読んだ印刷工程が実際に見られて感動。やっぱり紙の本はいい。置き場所があれば全部紙の本にしたい。

www.youtube.com

高慢と偏見（ジェイン・オースティン）

河出文庫版。訳がとてもよかった。長年なぜかジェイムズ・ジョイスの作品と勘違いしており、取っ付きにくい印象を持っていたが、実際に読んでみると全くそんなことはなかった。内容は少女漫画的で、結婚するかしないかで大騒ぎする話なので、個人的には苦手なジャンルのはずなのに、とても面白く読めた。そのうちに本作のパロディ映画『高慢と偏見とゾンビ』も観たい。また、2017年に中公文庫から19世紀の挿絵付き新訳がでたようだ。こちらも見てみたい。

夜と霧（ヴィクトール・E・フランクル）

徹底的に感情を排して書かれているのだが、著者が強制収容所から生還したあとに遭遇した悲劇を知ると、なんとも物悲しく、やりきれない。ちょうど一年前の正月に実家で読んだ。

高野聖（泉鏡花）

角川文庫版。いま出版社ページを見にいったら謎のキャラクターが表紙に書かれていたので、リンクは貼らないでおこう...... 短編集で、お気に入りは「義血侠血」。昔から『楢山節考』（深沢七郎）とか『愛と死』（武者小路実篤）とか『狭き門』（アンドレ・ジッド）とか、この手の（？）悲劇がどうもツボなようだ......

弥生美術館の「文豪・泉鏡花×球体関節人形」も見に行った。

bijutsutecho.com

衝撃だったのが「陽月」という方の作品（下記Instagram参照）で、現実離れした美しさに感動してしまった。ナボコフが書いたニンフェットはこんな感じなのだろうか。誇張でなく「吸い込まれそうな魅力」で、一日中見ていても飽きないと思う。この魅力は写真だと減衰する。それほど実物の存在感は圧倒的だった。彫りが深いので、泉鏡花作品の女性がこんな感じかと言われると、違うような気がするが......

www.instagram.com

展示会の内容を紹介する動画にも登場しているけど、やっぱり実物の方が魅力的。

www.youtube.com

面白かった映画

CABIN

古今東西のホラーのパロディのような映画。ホラー映画をよく見るのでかなり楽しめた。

ファイト・クラブ

有名なのは知っていたけど全く内容を知らなかった。思っていた映画と全然違って驚いた。冒頭のシークエンスからしてかっこいい。ラストシーンも大好き。

ジェイコブス・ラダー

始終暗く絶望的な雰囲気が漂う。こういう雰囲気の映画は大好物。Silent Hillはこの映画に強く影響を受けていると言われているが、確かに空気や演出が似ている。BD買う予定。

面白かったゲーム

Nintendo Switchを買ったり、機械学習用のPCを買うという名目でゲーミングPCを買ってSteam沼に沈みかけたせいで、数年ぶりにかなりの時間をゲームに費した。

GOROGOA

絵画のようなパズルゲーム。これまで遊んだゲームの中で一番美麗だと思う。初見でも1時間程度でクリアできるが、密度が濃い。

Bayonetta, Bayonetta 2

Switch版でクリアして、PC版も買ってしまった。敵キャラのデザインや登場演出が最高に好き。

Final Fantasy XV

かなりはまった。買ったPCに比較的高性能のGPU (GTX 1070 Ti) を積んでおいてよかったと心から思った。発表から発売まで10年以上かかっていたり、DLCの開発が中止されたりしたため、一部Web上には怨嗟の声が渦巻いているが、個人的にはかなり楽しめた。ストーリーはクリアしたが今も時々遊んでいる。2016年の発売当時とは違い、バグの修正や演出強化が行われたため、特に不満もなくプレイできている。

NieR:Automata

すごい世界観のゲームだ...... Cエンドでは泣いてしまった。サウンドトラックも買って、夜間ジョギングするときに聴いているが、ビル群が崩壊しつつある廃墟に見えてくる。Cエンドを見たあと最初からやり直しているが、ポッド強化用アイテムがなかなか手に入らないので苦労している。

ゼルダの伝説 ブレス オブ ザ ワイルド

今世紀最高のゲームの一つだと思う。コンサートにも行った。祠はコンプしてマスターバイク零式まで手に入れたところ。コログ集めはまだ200体程度......

Splatoon 2

今世紀最高のゲームの一つだと思う。ウデマエは全ルールS程度。サーモンランも楽しい。オクト・エクスパンションもクリア済み。今でもフェスには参加している。定期的にアップデートしてくれる公式には感謝しかない。

2019年もよく学び、よく遊びたい。

CourseraのMachine Learningを修了した

昨年のことだが、Courseraの有名なオンライン講義Machine Learningを修了した。講師はAndrew Ng氏。 www.coursera.org

このコースが公開されたのは2012年で、公開された直後にその存在をTwitterで知ったのだが、当時は別分野の研究のキャッチアップに必死で、興味はあったが受講している余裕がなかった。それからあっという間に6年の月日が経ち、ようやく受講して修了することができた。

「深層学習」が大流行の昨今において、今このコースを受講する価値があるかというと、大いにあると思う。当たり前だが「深層学習」はなんでもかんでも便利に解決してくれる魔法ではないし、多くのタスクにおいては、このコースで学ぶ深層学習以前の手法で十分だったりする。また、このコースは機械学習の手法を実サービスで利用する上での工夫や落とし穴を丁寧に教えてくれるため、単なる教科書以上の価値がある。

コースの内容については、6年の間にたくさんの受講者が記事を書いているのでここではふれない。難易度については、ごく初歩的な微分積分と線形代数の基礎を知っていれば全く問題ない。個人的に最大の障壁は課題で利用するOctaveだったが、慣れてしまえば大変便利である。

このコースが人気である理由の一つは、そのわかりやすさにあると思う。これまで受けたいくつかのオンライン講義を思い出すと、わかりにくいと感じた講義は、重要な観点を口頭で一回しか説明していないことが多かった。それに比べてNg氏は、重要な観点について言葉を変えつつなんども繰り返してくれるので、頭に残りやすいし理解しやすかった。また、Ng氏の誠実で熱意ある話し方も理由の一つだろう。修了した人のブログを読むと、最後の修了者向けメッセージで泣いてしまう人もいるようだ。

続編的なコースも公開されている。今は別の講義を受講しているが、そちらが一段落ついたらこちらも受講したい。 www.coursera.org

CourseraのParallel, Concurrent, and Distributed Programming in Java Specializationを修了した

Rice UniversityのParallel, Concurrent, and Distributed Programming in Java Specializationを修了した。

www.coursera.org

名前の通り、このSpecializationは以下の3つのコースからなる。

  • Parallel Programming in Java
  • Concurrent Programming in Java
  • Distributed Programming in Java

前回言及したのは最初のコースである。残りの2つも無事修了したので、晴れて全課程完了となった。 備忘のために2つのコースでの学習内容を引用しておく。

Concurrent Programming in Java

個人的に3つのコースの中で一番ためになった。

  • 1週目

    In this module, we will learn about threads and locks, which have served as primitive building blocks for concurrent programming for over five decades. All computing platforms today include some form of support for threads and locks, and make them available for use by developers in a wide range of programming languages. We will learn how threads can be created, joined, and synchronized using structured (e.g., synchronized statements/methods) and unstructured (e.g., java.util.concurrent libraries) locks in Java. We will also learn about new classes of bugs that can arise when concurrent programs need to access shared resources. These bugs are referred to as violations of liveness/progress guarantees, and include deadlock, livelock, and starvation. We will conclude this module by studying different solutions to the classical "Dining Philosophers" problem, and use these solutions to illustrate instances of deadlock, livelock and starvation.

Deadlock, livelock, starvationという重要概念が紹介される。また形式検証や並列プログラミング界隈でよく目にする"Dining Philosophers"問題にもふれる。

  • 2週目

    In this module, we will learn different approaches to coordinating accesses to shared resources without encountering the deadlock or livelock bugs studied earlier. Critical/isolated sections are higher-level concurrent programming constructs (relative to locks) that simplify the implementation of mutual exclusion by guaranteeing the absence of deadlocks and livelocks. Object-based isolation relaxes the constraints imposed by critical sections by allowing mutual exclusion to be specified on a per-object basis, as illustrated in the Spanning Tree example. Java's atomic variables represent an important, but restricted, case of object-based isolation that is implemented efficiently on all hardware platforms. Finally, we will learn how object-based isolation can be further relaxed with read/write access modes.

Intersection Emptinessを毎回判定して、共通部分が空ならdeadlockを気にせず並列処理できます、という手法が紹介される。Intersection Emptinessは場合によっては計算量が爆発するので気を付ける必要がありそう。また、基本的なatomic操作はCPUに専用命令が用意されているので高速だと知る。

  • 3週目

    In this module, we will learn another high-level approach to concurrent programming called the "Actor" model. A major difference between the Actor model and the Isolated Sections model is that there are no data races possible in the Actor model because it does not allow for any form of shared variables. However, as in all concurrent programming models, higher-level forms of nondeterminism are still possible in the Actor model due to an inherent asynchrony in the order in which messages may be delivered. We will study multiple examples of concurrency using the Actor model, including the classical Sieve of Eratosthenes algorithm to generate prime numbers, as well as producer-consumer patterns with both unbounded and bounded buffers.

アクターモデルの紹介。Producer-Consumer patternはエンタープライズ分野で頻出。よくキューが詰まって問題になっている印象。

  • 4週目

    In this module, we will study Concurrent Data Structures, which form an essential software layer in all multithreaded programming systems. First, we will learn about Optimistic Concurrency, an important multithreaded pattern in which two threads can "optimistically" make progress on their assigned work without worrying about mutual conflicts, and only checking for conflicts before "committing" the results of their work. We will then study the widely-used Concurrent Queue data structure. Even though the APIs for using concurrent queues are very simple, their implementations using the Optimistic Concurrency model can be complex and error-prone. To that end, we will also learn the formal notion of Linearizability to better understand correctness requirements for concurrent data structures. We will then study Concurrent Hash Maps, another widely-used concurrent data structure. Finally, we discuss a concurrent algorithm for finding a Minimum Spanning Tree of an undirected graph, an algorithm that relies on the use of Concurrent Data Structures under the covers.

楽観ロックやConcurrent Hash Mapの紹介。いづれもエンタープライズ分野で頻出。

Distributed Programming in Java

このコースはHadoop、Spark、Kafka、OpenMPIといった定番OSSの紹介が主で、コーディング課題はこれらのOSSに軽くふれるものだった。デモビデオの内容をほぼそのまま写経すれば課題クリアとなるので、これまでのコースの中で一番簡単だった。

  • 1週目

    In this module, we will learn about the MapReduce paradigm, and how it can be used to write distributed programs that analyze data represented as key-value pairs. A MapReduce program is defined via user-specified map and reduce functions, and we will learn how to write such programs in the Apache Hadoop and Spark projects. The MapReduce paradigm can be used to express a wide range of parallel algorithms. One example that we will study is computation of the TermFrequency – Inverse Document Frequency (TF-IDF) statistic used in document mining; this algorithm uses a fixed (non-iterative) number of map and reduce operations. Another MapReduce example that we will study is parallelization of the PageRank algorithm. This algorithm is an example of iterative MapReduce computations, and is also the focus of the mini-project associated with this module.

HadoopとSparkの違いがわかってよかった。両方ともMapReduceパラダイムに基づいた分散処理用のフレームワークだが、SparkはHadoopよりもメモリを積極的に使うことで、より効率的な分散処理を実現しようとするもの。

  • 2週目

    In this module, we will learn about client-server programming, and how distributed Java applications can communicate with each other using sockets. Since communication via sockets occurs at the level of bytes, we will learn how to serialize objects into bytes in the sender process and to deserialize bytes into objects in the receiver process. Sockets and serialization provide the necessary background for the File Server mini-project associated with this module. We will also learn about Remote Method Invocation (RMI), which extends the notion of method invocation in a sequential program to a distributed programming setting. Likewise, we will learn about multicast sockets,which generalize the standard socket interface to enable a sender to send the same message to a specified set of receivers; this capability can be very useful for a number of applications, including news feeds,video conferencing, and multi-player games. Finally, we will learn about distributed publish-subscribe applications, and how they can be implemented using the Apache Kafka framework.

オブジェクトのシリアライズ/デシリアライズを利用して、いわゆる「クラサバ」アプリを作成する方法が解説される。エンタープライズ分野で非常によくみる構成だが、Javaのシリアライズ/デシリアライズやRemote Method Invocation (RMI)は深刻な脆弱性の泉源となってきたので、実際に使用する場合は十分に注意しなければならない。以下の記事によると、Oracleはこれら「リスキー」な機能を根本的に見直そうとしているらしい。 www.infoworld.com

  • 3週目

    In this module, we will learn how to write distributed applications in the Single Program Multiple Data (SPMD) model, specifically by using the Message Passing Interface (MPI) library. MPI processes can send and receive messages using primitives for point-to-point communication, which are different in structure and semantics from message-passing with sockets. We will also learn about the message ordering and deadlock properties of MPI programs. Non-blocking communications are an interesting extension of point-to-point communications, since they can be used to avoid delays due to blocking and to also avoid deadlock-related errors. Finally, we will study collective communication, which can involve multiple processes in a manner that is more powerful than multicast and publish-subscribe operations. The knowledge of MPI gained in this module will be put to practice in the mini-project associated with this module on implementing a distributed matrix multiplication program in MPI.

Single Program Multiple Data (SPMD)が紹介される。MPIに関わると地獄、みたいな言説をTwitterで見かけたがどうなんでしょう。

  • 4週目

    In this module, we will study the roles of processes and threads as basic building blocks of parallel, concurrent, and distributed Java programs. With this background, we will then learn how to implement multithreaded servers for increased responsiveness in distributed applications written using sockets, and apply this knowledge in the mini-project on implementing a parallel file server using both multithreading and sockets. An analogous approach can also be used to combine MPI and multithreading, so as to improve the performance of distributed MPI applications. Distributed actors serve as yet another example of combining distribution and multithreading. A notable property of the actor model is that the same high-level constructs can be used to communicate among actors running in the same process and among actors in different processes; the difference between the two cases depends on the application configuration, rather the application code. Finally, we will learn about the reactive programming model, and its suitability for implementing distributed service oriented architectures using asynchronous events.

なんとこのSpecializationも終盤になってようやくプロセスとスレッドの違いが解説される。reactiveモデルにもややふれる。

結論

Javaに限らず、並列コンピューティングの概要を体系的に学びたかったので、広く浅くさまざまな概念を学べるこのSpecializationは非常に有益だった。定期的に復習して忘れないようにしたい。

Coursera Parallel Programming in Javaを受講した

社会人になるまでなんとなく Java を避けていたが、必要に迫られて学びはじめてみると、周辺ツールやライブラリ、学習資料が非常に充実していて驚いた。学生の頃はわからなかったが、いまなら Java がエンタープライズ分野で使われる理由がよくわかる。

4月に Coursera からコースの案内メールが来た。Rice University が提供する、Parallel, Concurrent, and Distributed Programming in Java Specialization というコースが紹介されていた。面白そうなので受講してみることにした。 www.coursera.org

今回修了したのは、その3つのクラスからなるコースの1つ目「Parallel Programming in Java」。4週間のクラスだったので、主に土日に1週分を学習し、4週ですべての課題を提出して修了条件を満たした。

コースの難易度は、同じ Coursera の有名クラス「Machine Learning」などと比べるとかなり簡単で、クラス毎に用意されたフォーラムの書き込みを見ると、2日程度ですべての教材と課題を消化した人もいるようだ。

クラス名に Java と入っているが、Java の並行処理ライブラリの使い方を懇切丁寧に解説するようなクラスではない。はじめに並列コンピューティングの概念を説明して、それを実現する Java の機能をさらっと紹介するという構成になっている。

各週の授業内容を公式ページから引用するとこんな感じだ。

  • 1週目

    We will learn about task creation, task termination, and the “computation graph” theoretical model for understanding various properties of task-parallel programs. These properties include work, span, ideal parallelism, parallel speedup, and Amdahl’s Law. We will also learn popular Java APIs for task parallelism, most notably the Fork/Join framework.

  • 2週目

    We will learn about futures, memoization, and streams, as well as data races, a notorious class of bugs that can be avoided with functional parallelism. We will also learn Java APIs for functional parallelism, including the Fork/Join framework and the Stream API’s.

  • 3週目

    We will start by learning how parallel counted-for loops can be conveniently expressed using forall and stream APIs in Java, and how these APIs can be used to parallelize a simple matrix multiplication program. We will also learn about the barrier construct for parallel loops, and illustrate its use with a simple iterative averaging program example. Finally, we will learn the importance of grouping/chunking parallel iterations to reduce overhead.

  • 4週目

    We will learn how Java’s Phaser API can be used to implement “fuzzy” barriers, and also “point-to-point” synchronizations as an optimization of regular barriers by revisiting the iterative averaging example. Finally, we will also learn how pipeline parallelism and data flow models can be expressed using Java APIs.

これだけ見ると盛り沢山の内容だが、それぞれがサラッと紹介される程度なので、並列コンピューティングの入門にはよい。深く学ぶには別の書籍なりオンラインコースが必要だろう。

修了条件を満たすには、毎週 mini project と呼ばれるプログラミング課題をクリアする必要がある。これも難易度は高くなくて、とくに1週目の project 以外は、ほぼ完成しているソースコードが提供されるため、それを少し改変すればよい。これには少々拍子抜けしたが、数ヶ月前に同クラスが開講された際のフォーラムの書き込みを見ると、そのときはすべて一からコードを書く必要があったようだ。

Mini project がなぜ今のような「お手軽」な形になったのかは不明だが、想像はできる。実は、この mini project は授業内容との乖離や、意図がわかりずらい出題になっている等の「問題」が少々ある。それらに対する問い合わせが殺到した結果、最初からある程度完成されたものを提供するようになったのではないだろうか。

個人的には気軽に楽しく受講できたので満足している。次の Concurrent Programming in Java も楽しみだ。

Ubuntu で『ソフトウェアの基礎』を読む

この記事は Ubuntu 14.04 上に Proof General と Coq をインストールし、Emacs から『ソフトウェアの基礎』を読む（実行する）ためのメモです。日本語の解説記事が見つからなかったので書きました。なお、筆者は Coq や Proof General に関して素人なので、誤りなどがありましたらご指摘いただけると幸いです。

Proof General と Coq のインストール

Emacs はインストールしてあるものとします。Proof General と Coq は以下の apt コマンドでインストールできます。

sudo apt install proofgeneral coq

補足: apt-get install ではなく apt install となっているのは誤りではありません。Ubuntu 14.04 から「aptコマンド」が使えるようになりました。詳細はこの記事をご参照ください。(2014/09/03 追記)

注意: 2014年8月31日現在、apt でインストールした Proof General のバージョンは 4.3pre130510 です。開発版は 4.3pre131011 のようですが、この記事では無視します。一方、インストールした Coq は 8.4pl3 ですが、最新版は 8.4pl4 です。8.4pl3 には重大なバグがあり、8.4pl4 で修正されたそうですが、近日中に 8.5 がリリースされる予定 (pdf) ということもあり、この記事では面倒を避けて古いものをそのまま使います。最新版を使いたいという方は以下の記事などをご参照ください。

『ソフトウェアの基礎』のソースをダウンロードして解凍

有志による日本語訳はこちらの「ソース」からダウンロードできますが、最終更新日が2011年6月とやや古いので、原文の方を以下のリンクからダウンロードします。なお、原文のバージョンは現時点で 3.1 (July 2014) です。

ダウンロードしてきたファイルを適当に解凍します。

tar zxvf sf.tar.gz

テキストを読んで実行

それでは、動作確認のために解答したフォルダの中の Basics.v を Emacs で開きます。

f:id:hark00:20140831021630p:plain:w500

光栄にも将軍が我々を歓迎してくれました。閣下のご尊顔を拝していると、Basics.v のバッファに自動で切り替わります。自動で移動しない場合は手動でバッファを切り替えてください。なお、環境によっては Proof General のツールバーが表示されているはずです。

f:id:hark00:20140831021814p:plain:w500

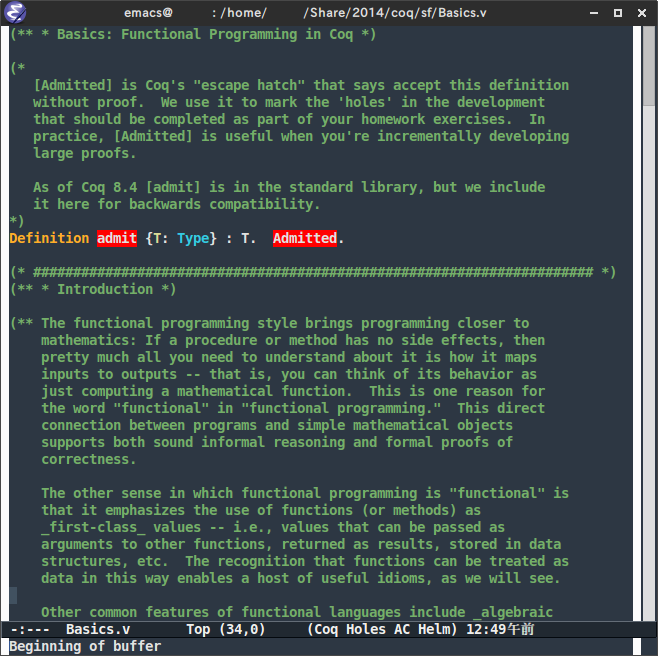
ふむふむと読んでいって Exercise 1 まで進めたとします。おんどりの導くままに正解と思うコードを入力し、そのコードの下あたりにカーソルを移動させたら、おもむろに C-c C-return を押します（つまり Ctrl を押したまま c を押し、次に Ctrl を押したまま Enter を押す）。

f:id:hark00:20140831021832p:plain:w500

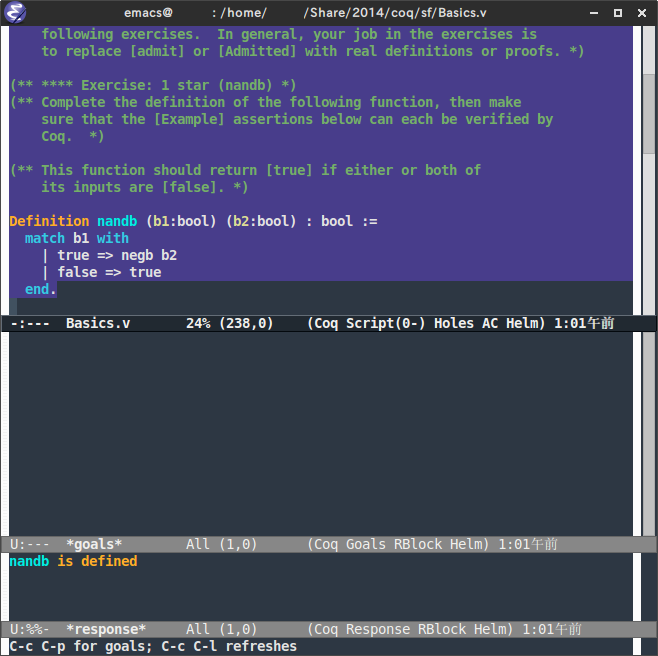
すると、カーソルより上の画面の背景の色が変わり、上図のように画面が3分割されます。一番下の画面 *response* に nandb is defined と表示されていればとりあえずOKです。文法などに誤りがある場合は *response* にエラーメッセージが表示されますので、コードを修正しましょう。

次に、自分で定義した nandb が正しいか確かめましょう。Exercise 1 の下に Example と (* FILL IN HERE *) Admitted. からはじまる文が並んでいます。本文に従って (* FILL IN HERE *) Admitted. を Proof. reflexivity. Qed. に書き換えたら、それらの行の下付近にカーソルを移動させて、再度 C-c C-return を押します。

自分で定義した nandb が正しければ背景の色が変わり、*response* には何も表示されません（あるいは test_nandb4 is defined などと表示されます）。nandb に誤りがあれば、エラーが出力されます。例えば以下のような:

Toplevel input, characters 0-11:
Error: Impossible to unify "true" with "nandb false false".

f:id:hark00:20140831022111p:plain:w500

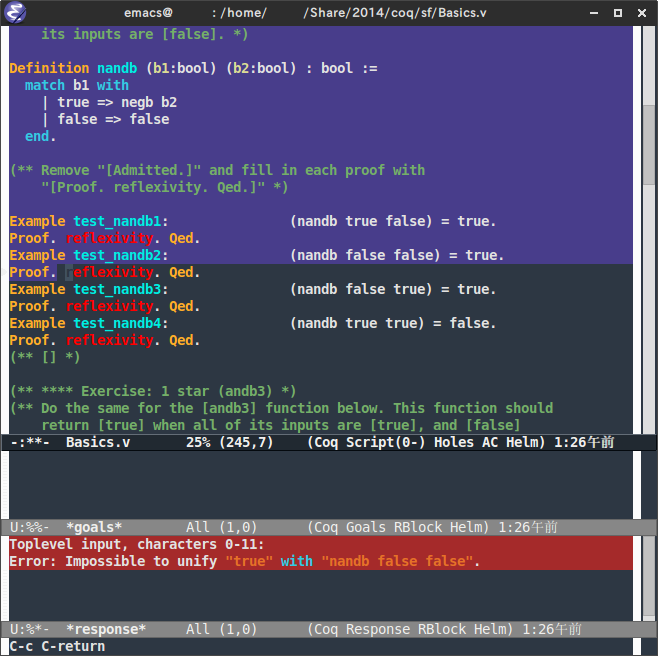
どうやら Example test_nandb2 でエラーが起きたようです。このテストが通るように nandb を書き直したら、再度 C-c C-return を押して正しさを確認しましょう。

まとめ

以上のように、『ソフトウェアの基礎』を読んで実行するときは、実行したい行にカーソルを移動させて C-c C-return を押せば大体やりたいことが実現できます。Check や Eval のある行も C-c C-return でOKです。

Proof General には他にも便利な機能がありますので、公式ページのドキュメントなどをご参照ください。よく使うキーバインドはこちらのページにまとまっています。

補足: Basics の中間付近からステップ実行が必須になります。ツールバーを利用してもよいですが、キーボードから操作できた方がなにかと便利ですので、1ステップ進む C-c C-n と1ステップ戻る C-c C-u をぜひ活用しましょう。また、Proof General の機能である Electric Terminator がオンになっていると、ピリオドを入力した際にその部分まで自動的に評価してくれます。機能のオン・オフは C-c . と押すことで切り替えられます。(2014/09/03 追記)

MATLAB の正規化周波数について

MATLAB の Signal Processing Toolbox を使っていると、このページの例のように横軸が「Normalized Frequency (正規化周波数)」になっているグラフが頻出する。しかし、MATLAB の正規化周波数は信号処理の教科書や技術書に書かれているものとやや異なる。そのため、使いはじめたばかりの学生（かつての自分含む）が混乱することがある。

実は、MATLAB の正規化周波数は「ナイキスト周波数」が基準となっている。以下、公式の FAQ から引用する。

This toolbox uses the convention that unit frequency is the Nyquist frequency, defined as half the sampling frequency. The cutoff frequency parameter for all basic filter design functions is normalized by the Nyquist frequency. For a system with a 1000 Hz sampling frequency, for example, 300 Hz is 300/500 = 0.6. To convert normalized frequency to angular frequency around the unit circle, multiply by π. To convert normalized frequency back to hertz, multiply by half the sample frequency. Frequency Response - MATLAB & Simulink


抄訳: Signal Processing Toolbox の単位周波数はナイキスト周波数であり、標本化周波数の半分です。(略) 標本化周波数が 1000 Hz ならば、300 Hz は（正規化周波数では）300/500=0.6 となります。正規化周波数を単位円上の角周波数に変換するには π を乗算し、ヘルツに変換するには標本化周波数の半分を乗算してください。

例

たいていの教科書では、正規化周波数は F = f / fs と書かれている。ここで f は周波数、fs は標本化周波数である。同様に正規化角周波数は Ω = ω / fs = 2πf / fs = 2πF と書かれている。この定義に基づいた教科書的な IIR フィルタの例を見てみよう。IIR フィルタの伝達関数は

\displaystyle H(z)=\frac{\sum^M_{m=0}a_mz^{-m}}{\sum^N_{n=0}b_nz^{-n}}

で与えられる。ここで z=e^{j\Omega}=e^{j2\pi F} として、ある低域通過フィルタの振幅特性を計算すると以下のようになる。

f:id:hark00:20140808193608p:plain:w250 f:id:hark00:20140808193613p:plain:w250

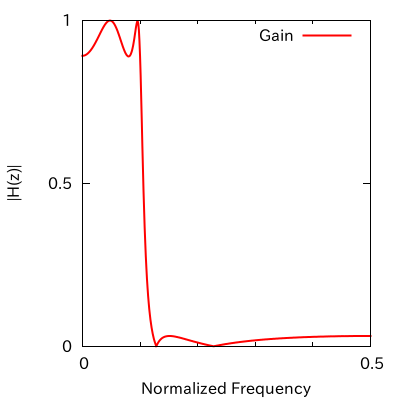
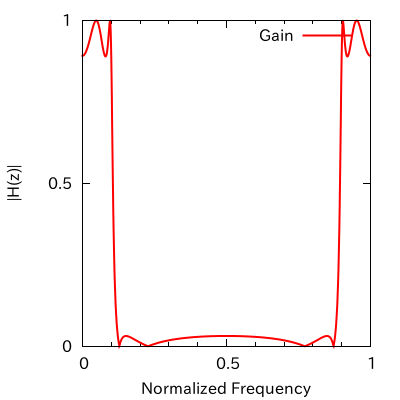
図の横軸は教科書的な正規化周波数である。左図は横軸を 0.5 まで、右図は 1.0 までとした。正規化角周波数に変換する場合は 2π を乗算すればよいので、0.5 は π、1.0 は 2π に変換される。

さて、標本化定理によると、標本化前の信号（原信号）の最大周波数が f のとき、原信号を標本化後の信号から正しく復元するためには、標本化周波数を 2f より大きくしなければならない。言いかえると、標本化周波数が fs ならば fs / 2 以上の周波数を持つ原信号は正しく復元できない。この標本化周波数の半分 fs / 2 をナイキスト周波数と呼ぶ。

冒頭で引用したように、MATLAB の正規化周波数はナイキスト周波数を基準としている。つまり、fs / 2 が単位周波数となるように設計されている。そのため上図では 0.5 であった横軸の点が 1.0 となる。下図のように。

f:id:hark00:20140808205525p:plain:w250

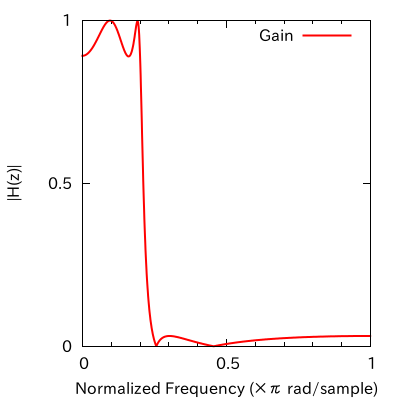
さきほどは正規化角周波数に変換するために 2π をかけたが、今回は π をかければよい。MATLAB の正規化周波数の単位が ×π rad/sample になっているのは、これが理由である。

なお、MATLAB に似た無料の数値計算ソフトである Scilab の正規化周波数は、自分の知るかぎり教科書通りである。そのため、使用に際して上記のような混乱はなかったと思う。

半環でグラフとサンバを

study

ちょっと前に半環とグラフに関する面白い話題を得たので、忘れないうちに書いておこうと思います。
猛暑がつづく悲しき亜熱帯に捧げる、トロピカルな記事です。

概要

一般に無閉路有向グラフ (DAG) は隣接行列の形で表すことができますが、隣接行列の累乗の和を計算すると、すべての二頂点間の経路重みの総和を計算することができます。実はこの計算過程をちょっと変えて、半環の一種であるトロピカル半環を用いると、すべての頂点間の最短経路が求められるというお話です。

隣接行列の積で経路重みの総和を計算

与えられた無閉路有向グラフ (以下、単にグラフ) のすべての二頂点間の経路重みの総和を計算しようと思ったとき、そのグラフの隣接行列の累乗の和を計算するという方法が使えます。ここで経路重みの総和とは、ある始点からある終点までの各経路について、同じ経路上の辺の重みを乗算し、それらの結果をすべて足し合わせたものとします。

例えば以下のような重み付きDAGを考えます。

f:id:hark00:20140801142038p:plain:w180

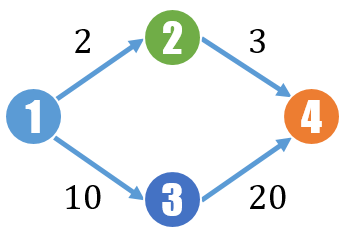
頂点 1 から頂点 4 までの経路は 2 本あります。それぞれの経路の重みは 2 × 3 = 6 と 10 × 20 = 200 で、これらを足した 206 が頂点 1 から頂点 4 までの経路の重みの総和です。

では、経路重みの総和をグラフの隣接行列の累乗の和から求めてみます。上図のグラフの隣接行列 M は以下のようになります。

M = \begin{pmatrix} 0 & 2 & 10 & 0 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 20 \\ 0 & 0 & 0 & 0 \end{pmatrix}

次に累乗の和を計算してみます。

M^{*} = \sum_{n\in\mathbb{N}} M^{n}

グラフの直径を r とすると、n > r の場合の M の n 乗は零行列になりますので、以下の計算では無視しています。上のグラフの直径は 2 なので、n = 2 まで計算すれば十分です。なお、閉路のあるグラフでは、n = k のとき長さ k 以下の経路の重みの総和が求められます。

f:id:hark00:20140804194304p:plain:w300

これですべての二頂点間の経路重みの総和が計算できました。図にある通り、頂点 1 から頂点 4 への経路重みの総和は、1 行目の 4 列目を見ればよいので、206 であることがわかります。

最短距離の計算

この節ではグラフの重みを距離と解釈します。前節での計算方法をちょっと変えると、ほぼ同じ手順で二頂点間の最短距離を求めることができます。変える部分は主に以下の3点です。

  • 0 を \infty で置換する
  • 行列の任意の2要素 x, y の乗算 xy の代わりに加算 x + y を計算する
  • 行列の任意の2要素 x, y の加算 x + y の代わりに min(x, y) を計算する

例で説明します。通常の行列の演算では、

A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix},\ B=\begin{pmatrix} 10 & 20 \\ 30 & 40 \end{pmatrix}

の加算と乗算は

A+B=\begin{pmatrix} 1+10 & 2+20 \\ 3+30 & 4+40 \end{pmatrix}, \ A\times B=\begin{pmatrix} 1\cdot 10 + 2\cdot 30 & 1\cdot 20 + 2\cdot 40 \\ 3\cdot 10 + 4\cdot 30 & 3\cdot 20 + 4\cdot 40 \end{pmatrix}

です。よって

A+B=\begin{pmatrix} 11 & 22 \\ 33 & 44 \end{pmatrix},\ A\times B=\begin{pmatrix} 70 & 100 \\ 150 & 220 \end{pmatrix}

となります。一方、上の変更を適用すると、行列間の加算は

A+B=\begin{pmatrix} \min(1,10) & \min(2,20) \\ \min(3,30) & \min(4,40) \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}

となり、また乗算は

A\times B=\begin{pmatrix} \min(1+10,2+30) & \min(1+20,2+40) \\ \min(3+10,4+30) & \min(3+20,4+40) \end{pmatrix} = \begin{pmatrix} 11 & 21 \\ 13 & 23 \end{pmatrix}

となります。では、このようなルールで M^* を計算してみましょう。

f:id:hark00:20140804195651p:plain:w300

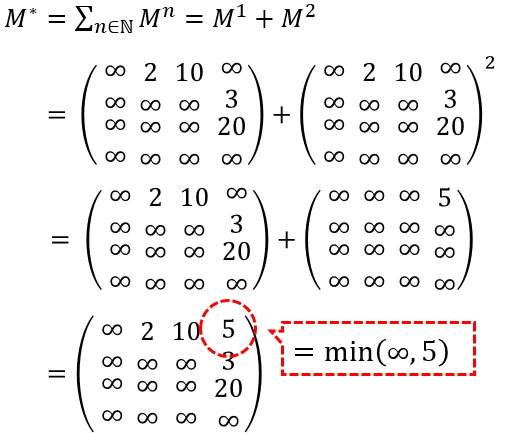
計算結果を見ると、行列の各要素が二頂点間の最短距離になっていることがわかります。1 行目の 4 列目は 5 ですが、これは頂点 1 から頂点 4 までの最短距離に対応しています。実際、上のグラフを見ると頂点 1 から頂点 4 までの最短距離は 2 + 3 = 5 となっています。

半環とトロピカル半環

経路重みの総和を求めた最初の例は、非負の実数上の4次正方行列半環を土台としており、最短経路を求めた例は、非負の実数上のトロピカル半環が土台です。

環はおおざっぱにいうと加法（加算）と乗法（乗算）の二種類の二項演算を持つ代数的構造です。また、加法的逆元を持たない環を半環と呼びます。
半環の中でも、加法として min を、乗法として + を持つ半環をトロピカル半環と呼びます。

上記の2つの例は加法と乗法の定義が異なっていただけで、計算の手続きは一緒でした。
ということは、経路重みの総和を計算するコードを書いておけば、重みに対する演算子のふるまいを変えるだけで、同じコードから最短経路が求められるようになります。かっこいい。

以上の話を発展させると「最短経路問題のための汎用アルゴリズム」が得られ、よく知られているダイクストラ法やベルマン・フォード法はこの汎用アルゴリズムの特殊な場合となります。
詳細は以下の論文をご参照ください。

  • Mohri, M. (2002). Semiring frameworks and algorithms for shortest-distance problems. Journal of Automata, Languages and Combinatorics, 7(3), 321-350. [ pdf ]